Graph reachability is one of the most fundamental concepts in graph theory and graph-based computing. At its core, it answers a deceptively simple question: can one node in a graph reach another node by following the edges? This question appears in countless domains, from determining whether a user can access a resource in a permission graph to analyzing dependencies in software systems or reasoning over knowledge graphs. Despite its apparent simplicity, reachability underpins many complex systems in computer science, data engineering, and artificial intelligence.

In graph-based systems, reachability is a core operation that determines how relationships are queried, analyzed, and exploited. Applications such as graph databases, recommendation systems, cybersecurity platforms, and semantic search engines rely heavily on efficient reachability queries. In many of these systems, multi-hop relationships encode the most valuable information, and reachability is often the first step toward extracting insight from those relationships.

This article provides a comprehensive explanation of graph reachability, explores its types and algorithms, and shows how it is applied in real-world systems, especially graph databases and knowledge graphs. It also discusses the challenges of reachability at scale and explains how PuppyGraph is designed to address those challenges in production environments.

What Is Graph Reachability

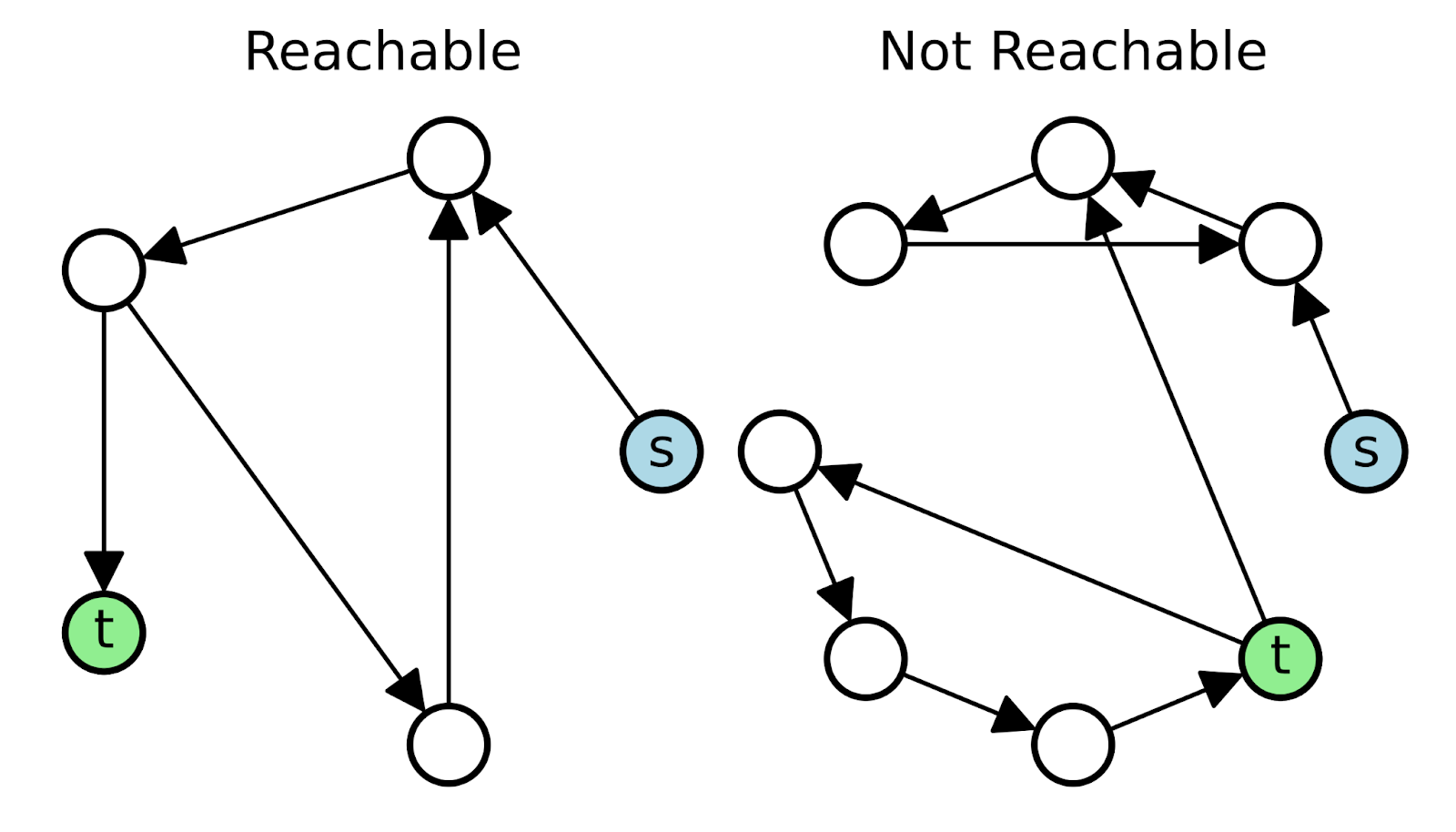
Graph reachability refers to the problem of determining whether there exists a path from one vertex (or node) to another within a graph. A path is defined as a sequence of edges that connects a starting node to a target node. If such a path exists, the target node is said to be reachable from the starting node. This definition holds regardless of whether the graph represents roads, hyperlinks, dependencies, or abstract semantic relationships.

Formally, given a graph \( G = (V, E) \), where \( V \) is the set of vertices and \( E \) is the set of edges, node \( v \) is reachable from node \( u \) if there exists a path \( u \rightarrow v \). The length of the path and the specific edges used are irrelevant to basic reachability; only the existence of a path matters. This makes reachability distinct from optimization problems such as shortest path, which consider distance, cost, or other metrics.

From a mathematical perspective, reachability defines a transitive relation over the nodes of a graph. If node A can reach B, and B can reach C, then A can reach C. This transitivity property is central to many forms of reasoning, including inheritance in ontologies, dependency resolution in software systems, and trust propagation in security models. Building on this property, the transitive closure of a graph can be defined as the reachability between all node pairs. 

In practice, reachability is rarely a one-off computation. Real systems often evaluate reachability repeatedly and at large scale. A production environment may need to answer millions of reachability queries per day across graphs containing billions of edges. This operational reality has driven extensive research into efficient algorithms, indexing strategies, storage layouts, and execution engines. Understanding reachability is therefore essential not only for theoretical computer scientists but also for engineers building graph-powered systems.

When to Use Graph Reachability

Graph reachability is used whenever the existence of a connection matters more than the quality, cost, or length of that connection. Many real-world problems are binary in nature: either something is accessible or it is not. In these cases, reachability provides exactly the information needed, without unnecessary computational overhead.

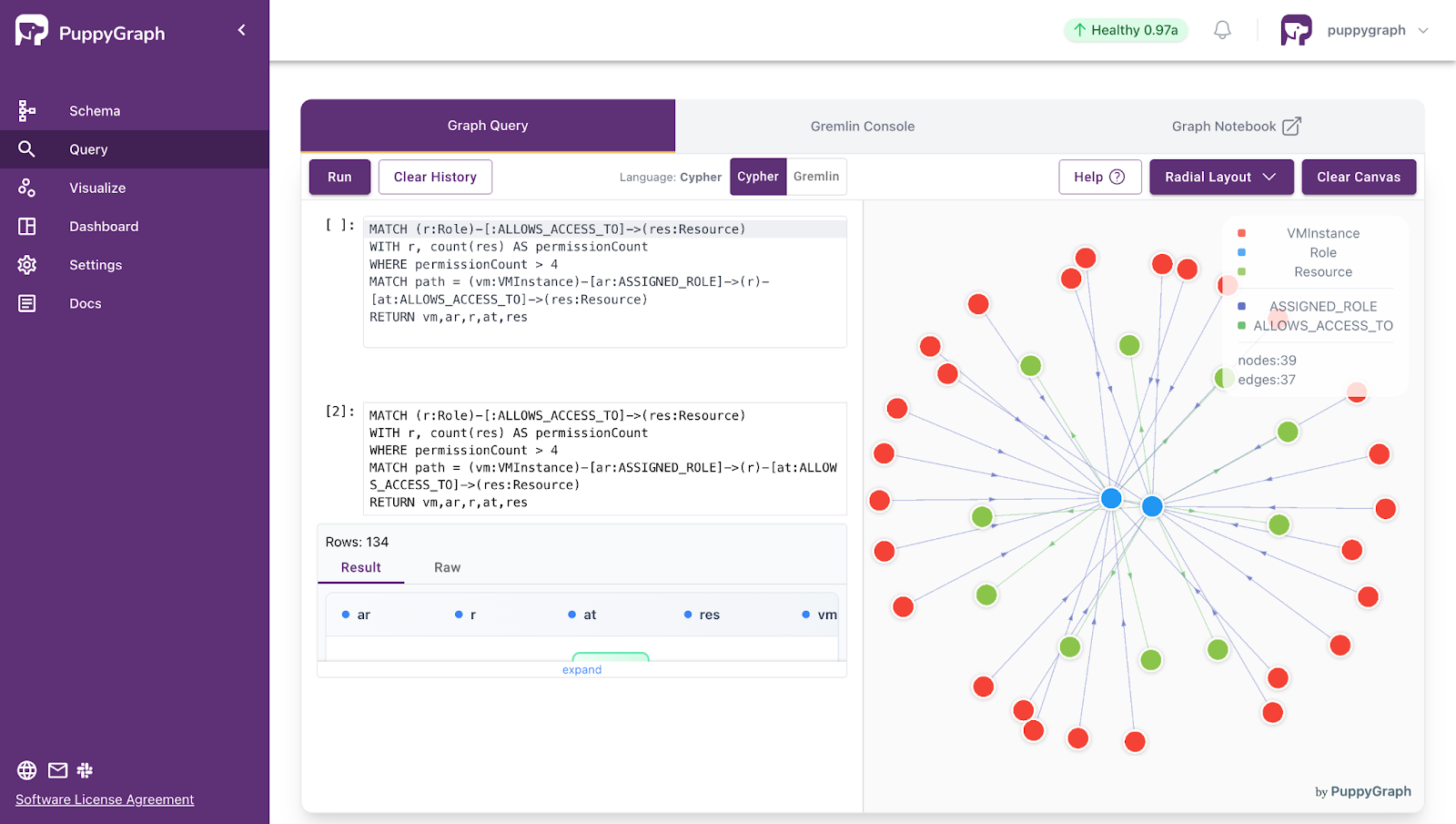
A classic example is access control and authorization. In enterprise systems, a user may inherit permissions through multiple layers of roles, groups, and policies. Determining whether a user can access a resource reduces to checking whether there is a path from the user node to the resource node through permission-granting edges. The system does not care how many steps the path has, only whether such a path exists.

In software engineering, reachability analysis is used to detect dead code or unused modules. Starting from an application entry point, such as a main function or API endpoint, engineers can determine which functions or classes are reachable. Any code that is not reachable from an entry point can be safely removed or flagged for further inspection. Similarly, in dependency management systems, reachability helps identify whether a package indirectly depends on a vulnerable library, even if that dependency is several layers deep.

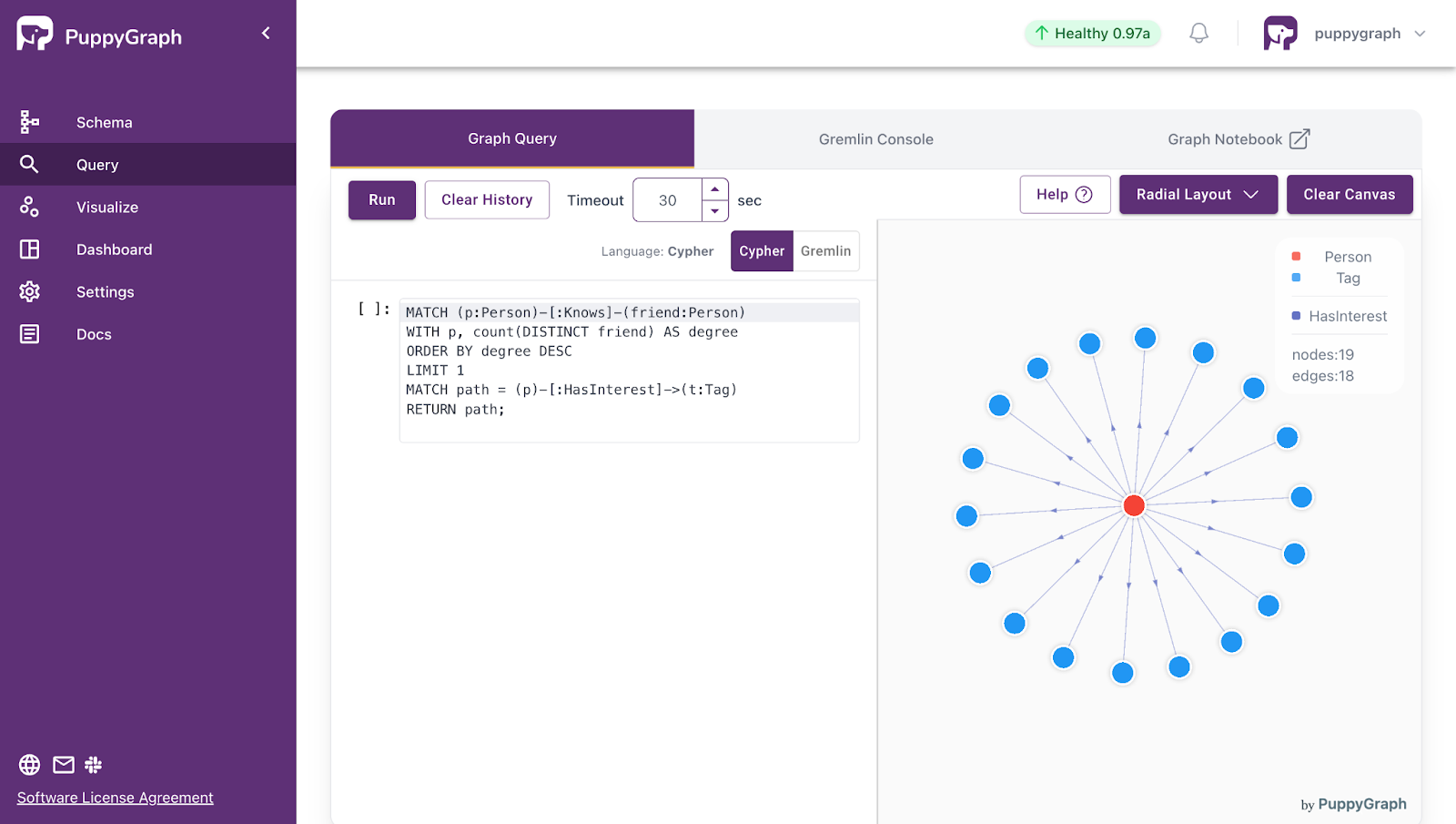
Reachability is also widely used in social network analysis. When analyzing relationships in large-scale social graphs, analysts often ask whether one user is connected to another user, possibly through multiple intermediaries. For example, determining whether two people are in the same social circle or whether information can spread from one account to another reduces to a reachability query. Graph reachability answers this question efficiently and forms the basis for friend recommendations, influence analysis, and misinformation containment.

In all these scenarios, reachability serves as a foundational query that enables higher-level reasoning and decision-making. It is often the first filter applied before more expensive computations or human investigation.

Types of Graph Reachability

Graph reachability can be categorized into several types depending on constraints, scope, and graph structure. One common distinction is between single-source reachability and all-pairs reachability. Single-source reachability asks which nodes can be reached from a given starting node, while all-pairs reachability considers reachability between every possible pair of nodes in the graph.

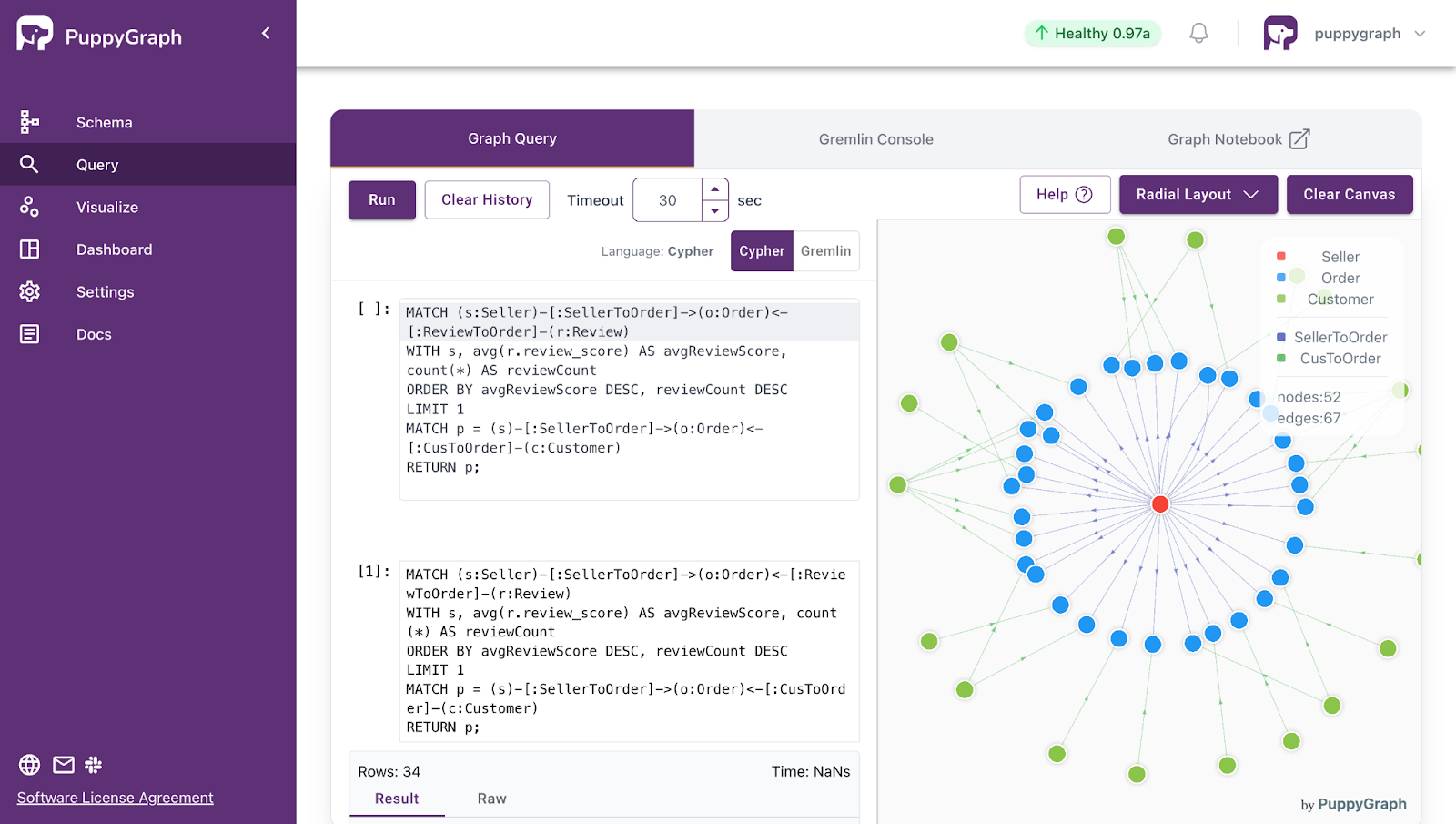
Another important category is conditional reachability, where paths must satisfy certain constraints. These constraints may involve edge labels, node properties, or path patterns. For example, in a transportation network, one might ask whether a city is reachable using only highways and excluding ferries. In a knowledge graph, a query might restrict traversal to specific relationship types such as is-a or part-of. Conditional reachability is especially common in graph databases and semantic systems.

Bounded reachability introduces limits on path length, such as asking whether a node is reachable within five hops. This is useful in scenarios like social network analysis, where influence or relevance tends to decay with distance. Bounded reachability balances expressiveness with performance by preventing unbounded graph exploration.

Temporal reachability arises in time-evolving graphs, where edges and nodes appear or disappear over time. In such graphs, reachability must respect temporal order: a path is valid only if its edges occur in a sequence consistent with time. Temporal reachability is important in event analysis, blockchain systems, and historical knowledge graphs.

These variations demonstrate that while the core idea of reachability is simple, it can be extended and adapted to solve complex real-world problems with nuanced constraints.

Graph Reachability in Directed and Undirected Graphs

The nature of reachability changes significantly depending on whether a graph is directed or undirected. In undirected graphs, edges have no orientation, meaning that if node A is connected to node B, then B is also connected to A. As a result, reachability in undirected graphs is symmetric: if A can reach B, then B can reach A.

In undirected graphs, reachability is closely related to the concept of connected components. All nodes within the same connected component are mutually reachable. Many problems in network analysis, clustering, and infrastructure planning rely on identifying these components.

In directed graphs, edges have a direction, and reachability becomes asymmetric. A node may be reachable from another without the reverse being true. This asymmetry is crucial for modeling real-world systems such as workflows, citations, data pipelines, and authority hierarchies, where relationships naturally flow in one direction.

Directed reachability often leads to the identification of strongly connected components, which are subsets of nodes where every node in the subset is reachable from every other node in the same subset by traversing the directed edges. Collapsing these components simplifies graph structure and enables more efficient reasoning. Understanding whether a graph is directed or undirected is therefore critical when choosing algorithms, interpreting results, and designing data models.

Common Graph Reachability Algorithms

Several classical algorithms are used to compute graph reachability, each with different performance characteristics and use cases. Breadth-First Search (BFS) is one of the most commonly used methods. Starting from a source node, BFS explores neighboring nodes level by level, marking all reachable nodes efficiently. BFS is often used when the shortest path length in terms of hops is also of interest.

Depth-First Search (DFS) is another fundamental algorithm that explores as far as possible along each branch before backtracking. DFS is particularly useful for tasks such as cycle detection, topological sorting, and computing strongly connected components, all of which are closely related to reachability.

Both BFS and DFS have linear time complexity with respect to the number of nodes and edges, making them efficient for single queries on moderately sized graphs. However, they become expensive when reachability queries are frequent or when graphs are extremely large.

When reachability queries extend beyond a single source to many node pairs, we need to compute the transitive closure of the graph. It can be computed using Floyd–Warshall algorithm, which is an elegant dynamic programming algorithm via three nested loops to determine whether a path exists between every pair of nodes.

Modern systems often combine these classical algorithms with indexing, pruning, and parallel execution to handle reachability at scale.

Graph Reachability in Graph Databases

Graph databases such as Neo4j, Amazon Neptune, and TigerGraph treat reachability as a first-class concern. Query languages like Cypher and Gremlin allow users to express reachability queries naturally using pattern matching and variable-length paths. For instance, consider a social network where nodes represent users and edges represent friendships. One might want to check whether “Alice” can reach “Bob” through any chain of friends within three hops. In Cypher, this can be expressed as:

MATCH (a:User {name: 'Alice'}), (b:User {name: 'Bob'})
MATCH path = (a)-[:FRIEND*1..3]->(b)
RETURN path

This query searches for all paths of up to three hops from Alice to Bob following FRIEND relationships. If the query returns a path, it confirms reachability within the specified limit; if not, no such connection exists. Beyond simple existence checks, reachability queries in graph databases can incorporate additional filters, such as edge types or node properties, and aggregations to analyze network connectivity, suggest friends, or detect isolated communities efficiently. This flexibility makes graph databases particularly suited for complex reachability analysis.

Graph Reachability vs Shortest Path

In graph theory, reachability and shortest path address related but fundamentally different questions. Reachability concerns only whether any path exists between two nodes, without regard to its length, cost, or efficiency. Shortest path problems, by contrast, seek an optimal path under a specified metric, such as distance, time, or weight.

From an algorithmic standpoint, BFS is a natural tool for graph reachability and can also compute shortest paths in graphs with unit edge weights. The Floyd–Warshall algorithm, while more commonly presented as an all-pairs shortest path algorithm, can be adapted to compute reachability between every pair of nodes, by ignoring edge weights and using Boolean operations. Because reachability tests are computationally cheaper, especially for single-source queries using BFS, they are often used as a preliminary filter before running more expensive shortest path algorithms.

Graph Reachability in Knowledge Graphs

Knowledge graphs model entities and their relationships to represent structured knowledge about the world, and reachability in knowledge graphs is essential for uncovering indirect relationships that are not immediately apparent.

For example, determining whether a medical condition is linked to a treatment through a chain of interactions: such as disease → symptom → biological pathway → drug, is fundamentally a reachability problem. By querying the graph for paths between nodes representing diseases and drugs, researchers can identify potential treatments or drug repurposing opportunities. 

Similarly, reachability plays a crucial role in ontology-based reasoning. In a biomedical ontology, for instance, one might want to check whether a specific protein is functionally related to a disease category through hierarchical subclass relationships. Here, reachability helps traverse the ontology’s taxonomy, connecting subclasses, superclasses, and annotated properties to answer complex queries. 

In both cases, reachability enables the discovery of hidden knowledge, supports hypothesis generation, and aids decision-making by exposing chains of relationships that are critical for scientific, clinical, or organizational reasoning.

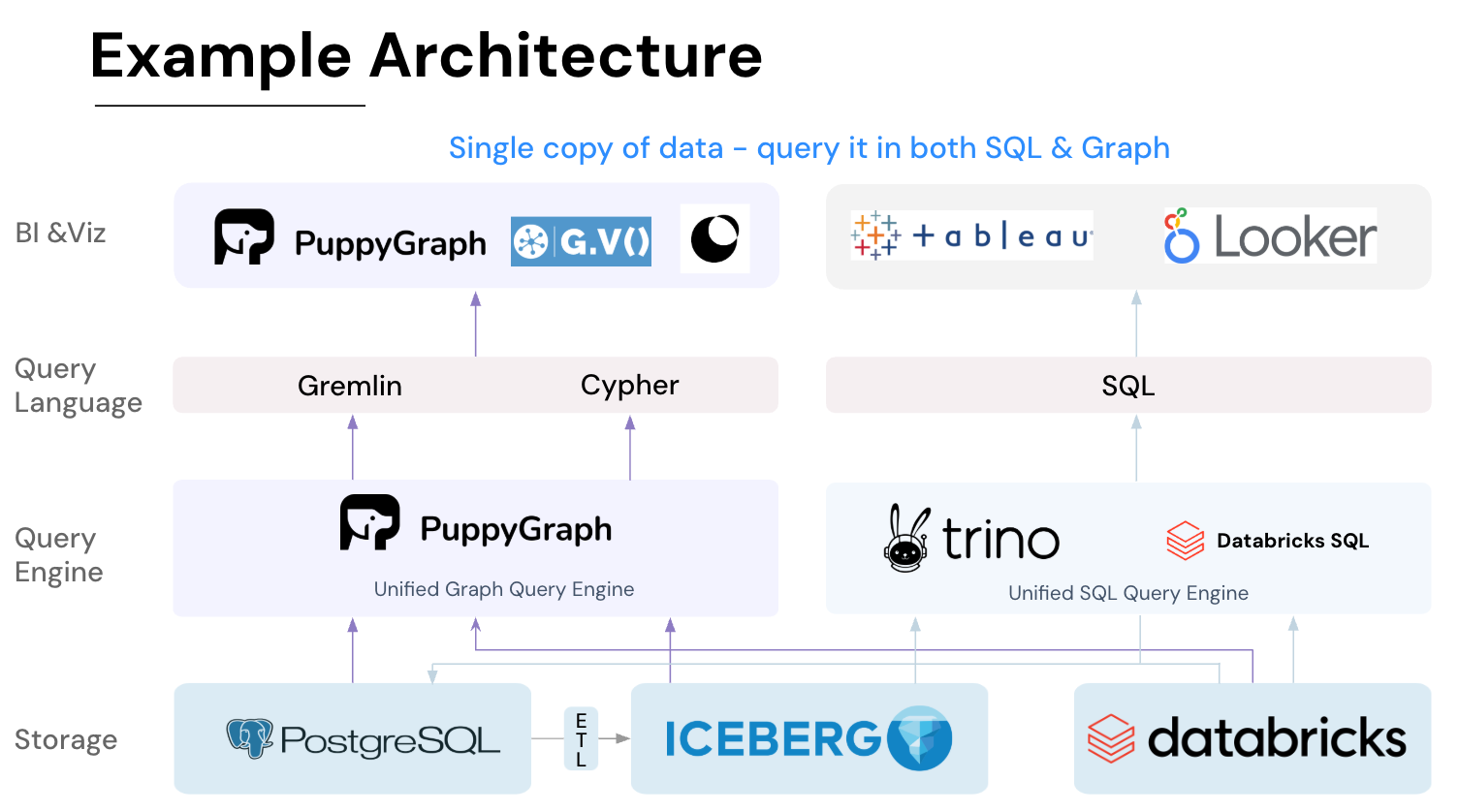
Graph Reachability with PuppyGraph

PuppyGraph supports both Gremlin and openCypher as query interfaces, allowing users to express reachability and traversal logic using standard graph query languages while operating directly on relational storage. In addition, PuppyGraph provides built-in support for reachability-related algorithms such as Weakly Connected Components (WCC) and Connected Component Finding.

These algorithms run directly over relational data and scale to very large graphs, allowing users to perform reachability-driven analysis without materializing graph snapshots or maintaining a separate graph store. Results can be accessed interactively or exported for downstream processing.

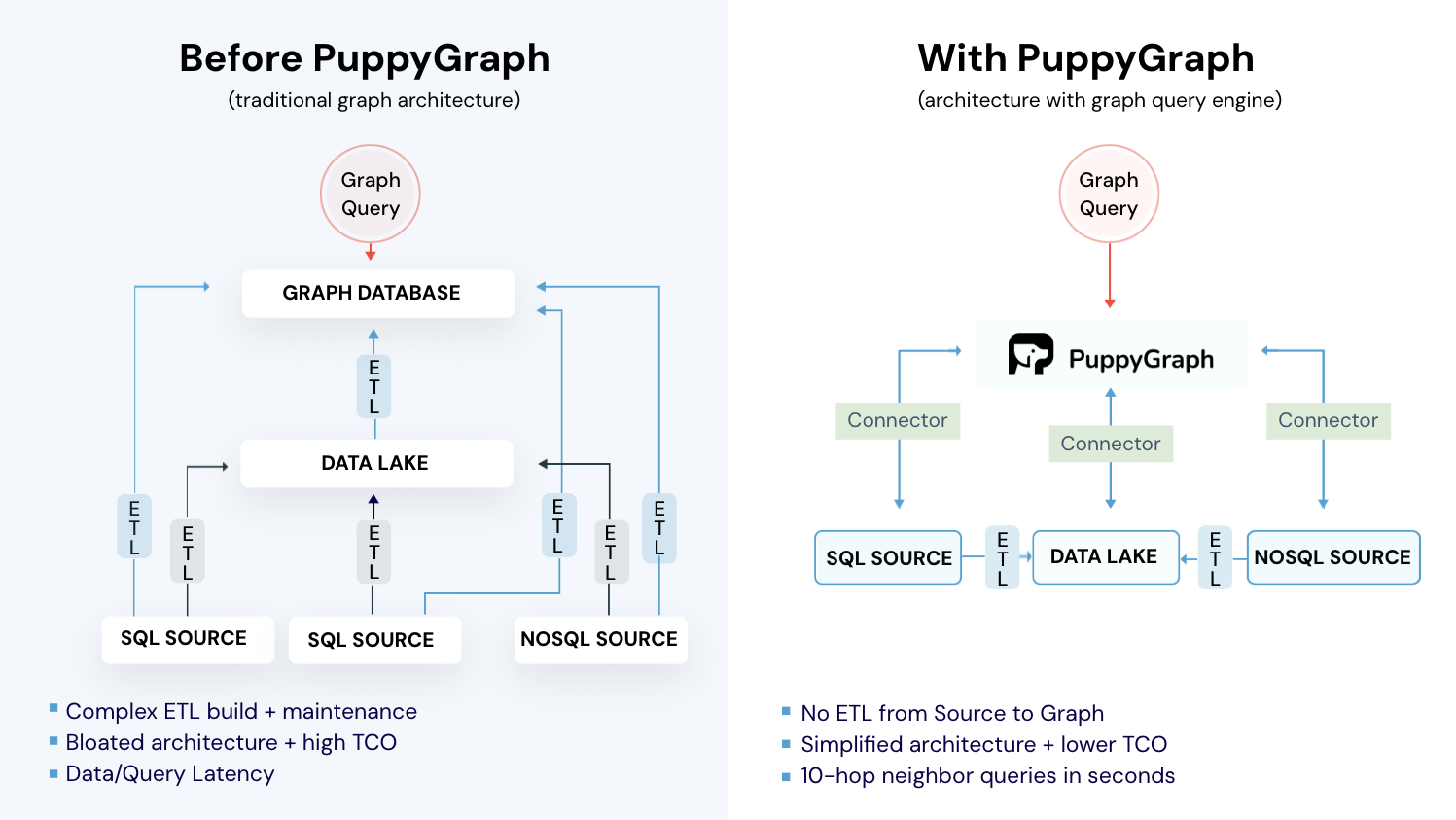
PuppyGraph is the first and only real time, zero-ETL graph query engine in the market, empowering data teams to query existing relational data stores as a unified graph model that can be deployed in under 10 minutes, bypassing traditional graph databases' cost, latency, and maintenance hurdles.

It seamlessly integrates with data lakes like Apache Iceberg, Apache Hudi, and Delta Lake, as well as databases including MySQL, PostgreSQL, and DuckDB, so you can query across multiple sources simultaneously.

Key PuppyGraph capabilities include:

• Zero ETL: PuppyGraph runs as a query engine on your existing relational databases and lakes. Skip pipeline builds, reduce fragility, and start querying as a graph in minutes.

• No Data Duplication: Query your data in place, eliminating the need to copy large datasets into a separate graph database. This ensures data consistency and leverages existing data access controls.

• Real Time Analysis: By querying live source data, analyses reflect the current state of the environment, mitigating the problem of relying on static, potentially outdated graph snapshots. PuppyGraph users report 6-hop queries across billions of edges in less than 3 seconds.

• Scalable Performance: PuppyGraph’s distributed compute engine scales with your cluster size. Run petabyte-scale workloads and deep traversals like 10-hop neighbors, and get answers back in seconds. This exceptional query performance is achieved through the use of parallel processing and vectorized evaluation technology. 

• Best of SQL and Graph: Because PuppyGraph queries your data in place, teams can use their existing SQL engines for tabular workloads and PuppyGraph for relationship-heavy analysis, all on the same source tables. No need to force every use case through a graph database or retrain teams on a new query language.

• Lower Total Cost of Ownership: Graph databases make you pay twice — once for pipelines, duplicated storage, and parallel governance, and again for the high-memory hardware needed to make them fast. PuppyGraph removes both costs by querying your lake directly with zero ETL and no second system to maintain. No massive RAM bills, no duplicated ACLs, and no extra infrastructure to secure.

• Flexible and Iterative Modeling: Using metadata driven schemas allows creating multiple graph views from the same underlying data. Models can be iterated upon quickly without rebuilding data pipelines, supporting agile analysis workflows.

• Standard Querying and Visualization: Support for standard graph query languages (openCypher, Gremlin) and integrated visualization tools helps analysts explore relationships intuitively and effectively.

• Proven at Enterprise Scale: PuppyGraph is already used by half of the top 20 cybersecurity companies, as well as engineering-driven enterprises like AMD and Coinbase. Whether it’s multi-hop security reasoning, asset intelligence, or deep relationship queries across massive datasets, these teams trust PuppyGraph to replace slow ETL pipelines and complex graph stacks with a simpler, faster architecture.

As data grows more complex, the most valuable insights often lie in how entities relate. PuppyGraph brings those insights to the surface, whether you’re modeling organizational networks, social introductions, fraud and cybersecurity graphs, or GraphRAG pipelines that trace knowledge provenance.

Deployment is simple: download the free Docker image, connect PuppyGraph to your existing data stores, define graph schemas, and start querying. PuppyGraph can be deployed via Docker, AWS AMI, GCP Marketplace, or within a VPC or data center for full data control.

Conclusion

Graph reachability is a foundational concept that enables systems to reason about connectivity, dependency, and influence across complex networks. From access control and software dependency analysis to social networks and knowledge graphs, reachability provides a simple yet powerful way to determine whether relationships exist, often serving as the first step toward deeper analysis. While the idea is conceptually straightforward, supporting reachability queries efficiently at scale requires careful algorithmic choices, data modeling, and execution strategies, especially in modern, large, and dynamic graphs.

PuppyGraph addresses these challenges by making reachability analysis fast, scalable, and practical in real-world production environments. By querying relational data in place with zero ETL and supporting standard graph query languages, it combines the strengths of SQL and graph computing. This approach allows teams to explore multi-hop relationships, perform real-time analysis, and uncover hidden connections without the cost and complexity of traditional graph databases.

Explore the forever-free PuppyGraph Developer Edition, or book a demo to see it in action.